[백준 - 1978] 소수 찾기
문제
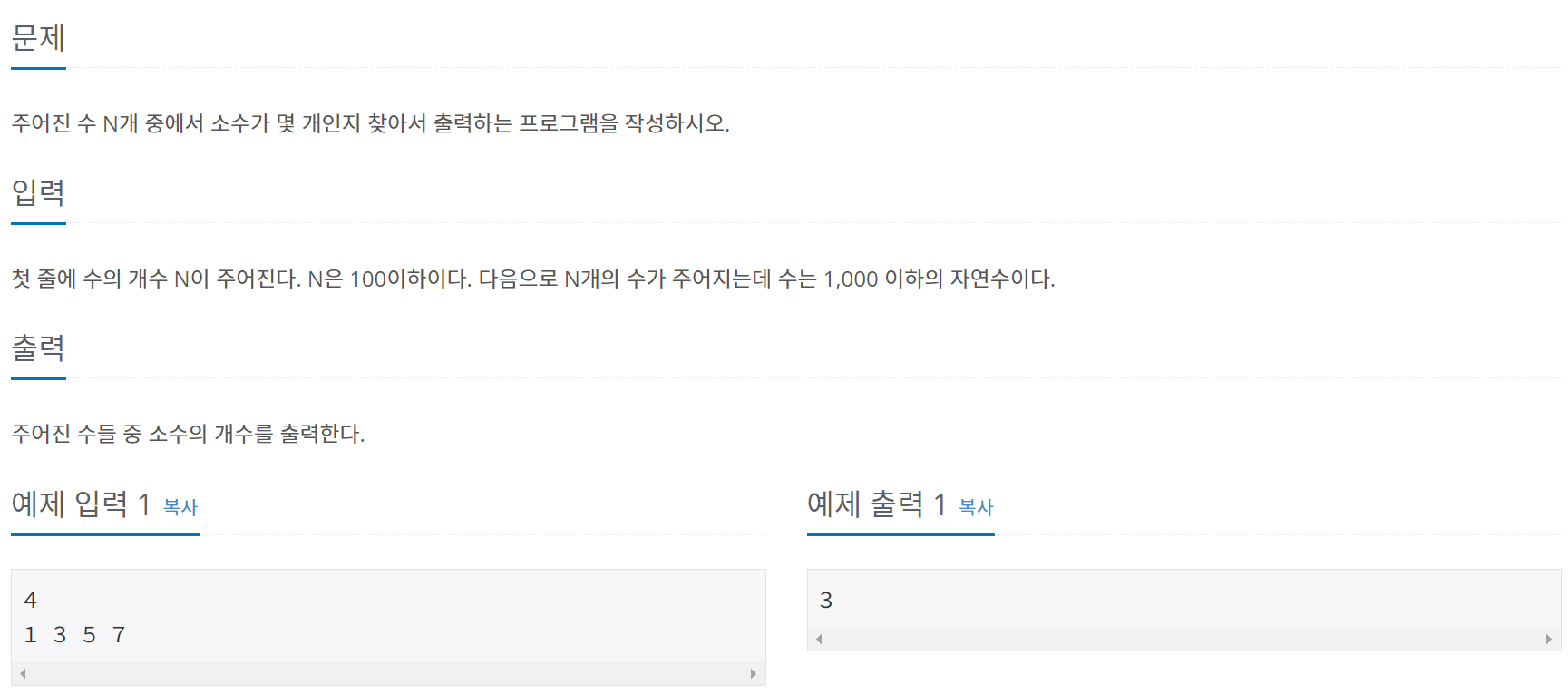
백준 1978번 소수 찾기 문제
소수 판별
소수💬 판별법 3가지에 대해 공부해보자.
소수는 약수로 1과 자기 자신만을 가지는 숫자를 말한다.
1. 기본적인 판별법
소수는 1과 자신만을 약수로 갖기 때문에 아래처럼 2부터 판별하려는 수 직전까지 하나씩 나눠서 판별하면된다.
private boolean checkPrime(int num) {
// 1은 소수가 아니므로 false
if(num == 1) return false;
for (int j = 2; j < Math.sqrt(num); j++) {
if(num % j == 0) return false;
}
return true;
}
이 방법의 경우 시간복잡도는 \(O(N\))이다.
2. 제곱근을 이용한 판별법
두번째 방법은 약수에 초점을 맞춰서 보는 방법이다.
예를 들어, 23을 판별한다고 해보자.
방법 1로 진행한다면 2부터 22까지 하나씩 나누어 나머지가 0으로 떨어지는 수가 있는지 검사할 것이다.
23 % 2 = 1 -> 약수 아님
23 % 3 = 2 -> 약수 아님
.
.
.
23 % 22 = 1 -> 약수 아님
∴ 23은 소수이다.
이렇게 2부터 판별 수의 직전까지 검사해야 한다.
작은 숫자라면 문제가 없지만 숫자의 크기에 비례해 판별하는데 시간이 오래 걸릴 것이다.
따라서, 판별수의 제곱근을 이용해 더 효율적으로 판별해 보자.
제곱근을 이용해 생각해 보면 23이라는 숫자를 판별할 때 5 이상의 수는 검사할 필요가 없다는걸 알 수 있다.
임의의 숫자 Number를 \(A * B\)의 합성수라고하면 아래와 같이 부등식을 세울 수 있다.
\(1 \le A, B < Number\)
여기서 만약 A와 B가 Number의 제곱근보다 크다면 위의 부등식에 모순이 생긴다.
\(A, B > \sqrt{Number} \Longrightarrow A * B > Number \)
위의 식은 \(A * B = Number\)라는 식과 모순이므로 다음과 같은 결론이 나온다.
∴ A와 B 중 적어도 하나는 Number의 제곱근보다 작거나 같다.
즉, 23의 제곱근은 약 4.8이므로 23을 5 이상의 수로 나눌 때 나누려는 숫자가 23의 제곱근보다 크기 때문에
몫은 23의 제곱근보다 작은 2, 3, 4가 되거나 나누어서 나머지가 0으로 떨어지지 않는 수가 된다.
따라서, 5 이상의 수를 검사할 필요 없이 4까지만 검사하면 된다.
아래처럼 코드로 표현할 수 있다.
private boolean checkPrime(int num) {
// 1은 소수가 아니므로 false
if(num == 1) return false;
for (int j = 2; j < Math.sqrt(num); j++) {
if(num % j == 0) return false;
}
return true;
}
이 방법의 경우 시간복잡도는 \(O(\sqrt{N}\))이다.
3. 에라토스테네스의 체
마지막 방법은 에라토스테네스의 체이다.
임의의 숫자 \(n_1\)부터 \(n_2\)사이의 소수를 구할 때 쓰면 좋은 방법이다.
방법은 간단하다.
체에 거르듯이 숫자를 걸러내면 된다.
아래의 그림을 보자
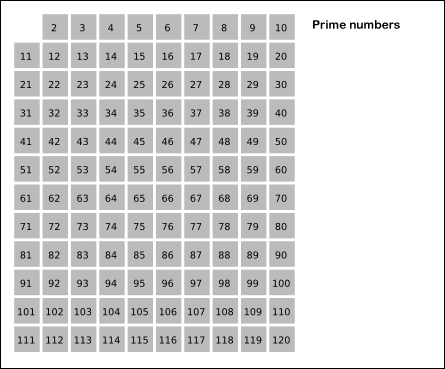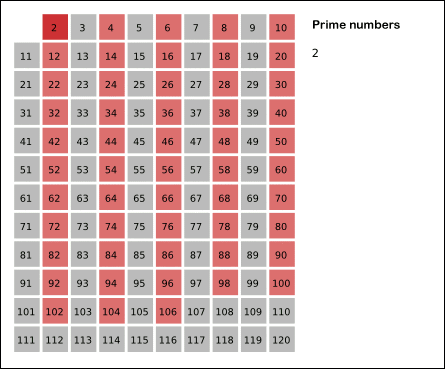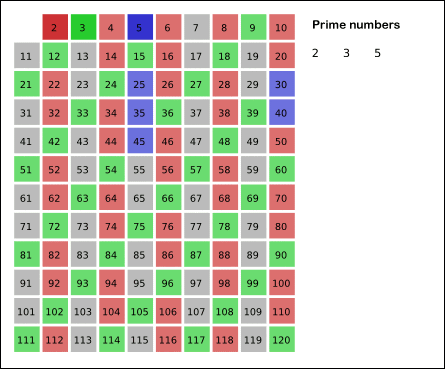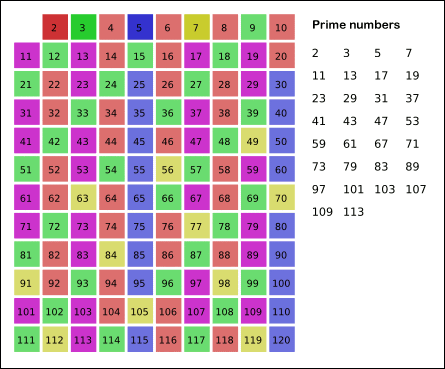
우선 2를 제외한 2의 배수를 모두 거르고, 그 다음 3을 제외한 3의 배수를 모두 거른다.
그 다음 4인데 4는 2의 배수로 걸러졌으므로 확인하지 않는다.
그 다음 5를 제외한 5의 배수를 모두 거른다.
이런 식으로 숫자를 하나씩 올려가며 앞서 나온 숫자의 배수로 걸러지지 않은 숫자는 소수로 남기고 그 숫자의 배수들을 걸러준다.
그리고 이 방법도 2번째 방법과 마찬가지로 제곱근을 이용할 수 있다.
구하려는 범위의 최댓값의 제곱근까지만 반복하며 된다.
100까지 구하려면 10까지 숫자를 확인하면 된다.
아래처럼 코드로 표현할 수 있다.
private boolean[] checkPrime(int num) {
boolean[] primeFlg = new boolean[num+1];
// 0과 1은 소수가 아니므로 true
primeFlg[0] = true;
primeFlg[1] = true;
for (int i = 2; i < Math.sqrt(num); i++) {
// 이미 걸러진 숫자라면 Pass
if(primeFlg[i]) continue;
//
for (int j = i * i; j < num+1; j = j + i) {
primeFlg[j] = true;
}
}
return primeFlg;
}
이 방법의 경우 시간복잡도는 \(O(n \log (\log n)\))이다.
방법 1과 방법2보다 시간복잡도가 안좋아보이지만, 이 경우는 0부터 \(num\)사이의 모든 소수를 구하기 때문이다.
범위 내의 모든 소수를 구할 때의 시간복잡도는 아래와 같다.
방법 1 : \(O(N^2\))
방법 2 : \(O(N\sqrt{N}\))
문제 풀이
방법 2를 사용해서 문제를 풀어보자.
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
int result = 0;
for (int i = 0; i < N; i++) {
int num = Integer.parseInt(st.nextToken());
// 1은 소수가 아니므로 continue
if(num == 1) continue;
boolean flg = true;
for (int j = 2; j < Math.sqrt(num); j++) {
if(num % j == 0) flg = false;
}
if (flg) result++;
}
System.out.println(result);
}
