개발하는 호랑이

반가워욤 :)

1 분 소요

문제

백준 9020번 골드바흐의 추측 문제

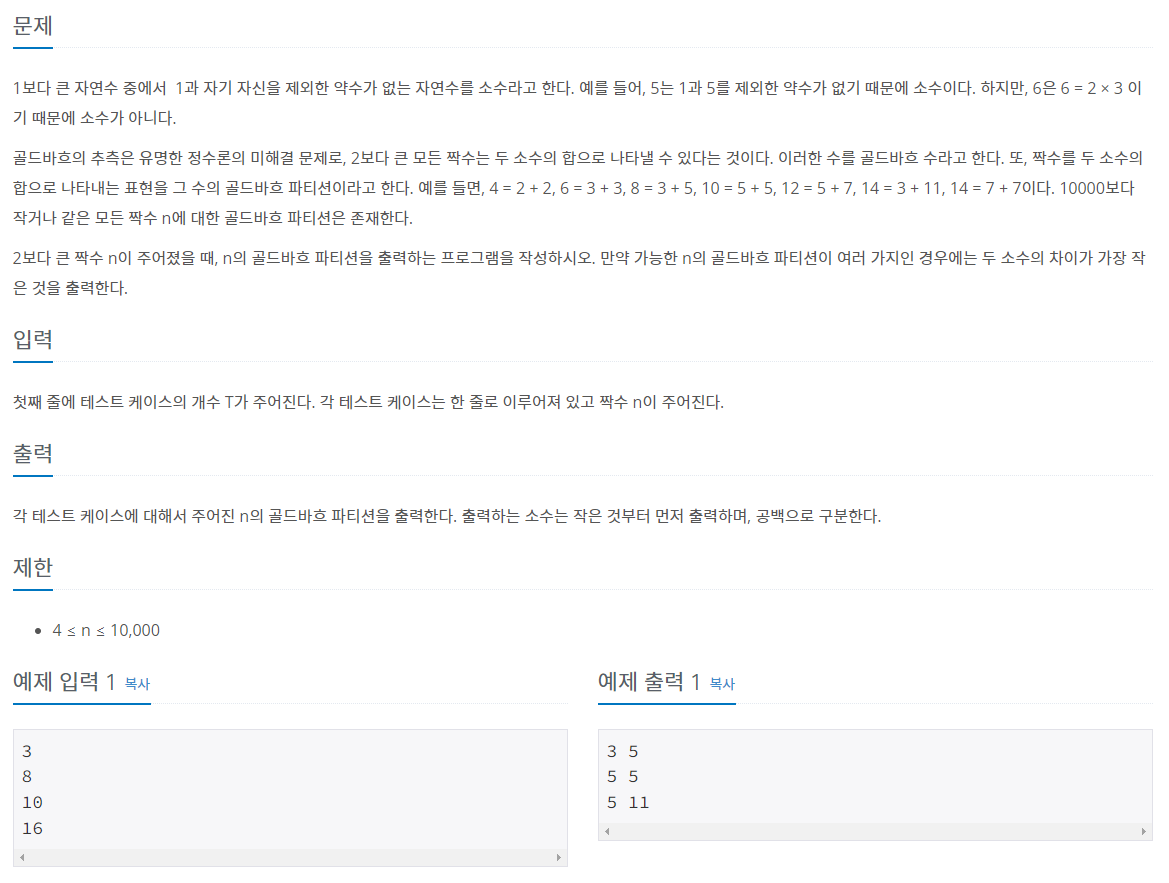
문제 풀이

문제는 소수찾기에서 사용했던 에라토스테네스의 체를 이용하면 된다.

1.

우선 에라토스테네스의 체를 통해 문제에 나와 있듯이 0 ~ 10000 까지의 소수를 구별하는 배열을 만든다.

public class Main {
	public static void main(String[] args) throws IOException {
		boolean[] primeFlg = new boolean[10001];
		primeFlg[0] = true;
		primeFlg[1] = true;
 
		for (int i = 2; i<= Math.sqrt(primeFlg.length); i++) {
			if (primeFlg[i]) continue;
			for (int j = i * i; j < primeFlg.length; j += i) {
				primeFlg[j] = true;
			}
		}
	}
}

2.

그 다음 문제의 조건을 보자.
문제에서 2보다 큰 짝수인 N이 주어졌을 때 합해서 N이 되는 두개의 소수를 구하고,
거기에 추가적으로 합해서 N이 되는 소수가 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 구하라 하였다.

예를 들어, 16이라는 수가 주어졌을 때 16은 (11 + 5 = 16) 또는 (13 + 3 = 16)의 경우의 수가 나올 수 있다.
이런 상황에서는 경우의 수 중에서 소수의 차이가 작은 경우를 출력해야한다.
차이가 가장 작은 두 소수를 구하기 위해 N을 2로 나누어서 두 소수를 1씩 줄이고 증가시켜 계산하면된다.

하나의 소수를 M 다른 하나의 소수를 B라고 하면 (M + B = N)이 되는데 M과 B를 N/2로 할당해주고,
M과 B를 확인해 두 수 모두 소수인지 확인한다. 만약 둘 다 소수가 아니라면 소수가 될 때까지 +1 또는 -1을 해주면 된다.
그렇게 조건이 성립할 때까지 각각의 숫자에 +1, -1을 해주다가 최초로 조건이 성립하는 순간의 M과 B를 출력한다.

예를 들어, 16을 반절로 나누어 더하면 (8 + 8 = 16)이다. 하지만 8은 소수가 아니므로 조건이 성립하지 않는다.
이렇게 조건이 성립하지 않으면 각각의 숫자에 +1, -1을 해준다. 그럼 (7 + 9 = 16)이 된다.
두 개의 수가 모두 소수가 될 때까지 이 과정을 반복하다보면 최초로 조건이 성립하는 (5 + 11 = 16)이 나온다.

결과적으로 아래처럼 코드를 작성하면 된다.

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
 
public class Main {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

 		boolean[] primeFlg = new boolean[10001];
		// 소수 판별할 배열 구하는 부분 생략

		int T = Integer.parseInt(br.readLine());
		StringBuilder sb = new StringBuilder();

		for (int i = 0; i < T; i++) {
			int N = Integer.parseInt(br.readLine());
			int M = N/2;
			int B = N/2;

			while (true){
				if(!primeFlg[M] && !primeFlg[B]){
					sb.append(M).append(" ").append(B).append("\n");
					break;
				} else {
					M--;
					B++;
				}
			}
		}
		System.out.println(sb);
	}
}

우선 테스트를 반복할 횟수인 T를 입력받고, 반복문안에서 목표 숫자인 N을 입력받는다.
위에서 설명했듯이 M과 B에 N/2를 할당해주고 반복문을 통해서 조건이 만족했을 때 StringBuilder에 값을 넣어준다.

참고하며 공부한 블로그

참고